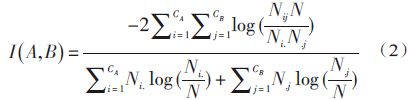在线社交网络的广泛应用使社交网络分析成为一个重要的研究领域,其在数据挖掘、信息传播、网络建模、行为分析、知识发现等领域中发挥着重要作用[1, 2, 3] 。在社交网络中,人们将连接相对紧密的群体视为社区。社区通常由功能相近或属性相似的用户组成,在一定程度上反映了社交网络的局部规则性和全局有序性。社区发现能有效揭示网络系统的中观特征及群体的共性规律,是解决复杂系统的基础,还有助于推进相关应用的发展,如朋友推荐、隐私保护、网络营销等。因此社区发现是社交网络分析领域的重要研究方向之一,对分析和理解社交网络结构属性、群体特征等方面具有重要意义。针对社区发现问题,目前已出现了大量的研究成果,可以分为全局优化和局部优化两大类。基于全局优化的社区发现方法主要从全局的角度划分整个网络,需要整个网络结构信息,目前主要包括图划分[4, 5] 、层次聚类[6, 7] 、模块度优化[8, 9, 10, 11, 12, 13, 14] 、谱聚类[15, 16] 及基于模型的方法等[5, 17, 18] 。全局方法存在一定的局限性:(1)从划分和聚类观点分析,对于待处理的网络,需要整个网络结构信息以及社区规模和社区划分数目等先验知识;(2)从计算复杂度来说,社交网络规模巨大并呈动态扩大趋势,全局搜索和计算必然会影响算法的运行速度和资源利用率;(3)从网络结构本身来说,运用全局划分方法不能从本质上发现社交网络中社区的重叠属性[19, 20] 。
基于局部结构优化的社区发现方法被提出,如局部扩展优化[20, 21, 22, 23, 24, 25] 、标签传播[26, 27, 28, 29, 30] 、派系过滤[19, 31, 32] 、局部边聚类优化[21, 33, 34] 等,并在社交网络分析中有广泛的应用。局部优化方法主要基于网络的局部拓扑结构特征,来揭示局部或整个网络的社区结构。与全局的社区发现方法相比,基于局部的方法无需完整的网络结构信息及先验知识的辅助就能有效发现社区,同时针对规模巨大、动态变化的在线社交网络,在计算代价、挖掘局部社区特性等方面存在更多优势[35, 36] ;最后,从社区本身来说,社区本质上是一个局部结构,包括所属模块的核心节点和其外围的邻居节点,这种社区特征在大规模社交网络中尤为明显,局部社区的形成仅基于网络中局部信息而非整个网络而构成。因此,基于局部优化的方法更适合解决社交网络环境下的社区发现问题。
鉴于上述,本文将对基于网络局部优化的各种社区发现技术的研究现状进行综述,介绍社区定义和评价指标;针对在线社交网络的特点,对基于局部优化的社区发现方法进行分析、比较;最后对社区发现研究中存在的问题和挑战做了探讨,并对未来的研究进行展望。2 社区定义与社区发现算法评价指标2.1 社区定义
迄今为止,一些研究者从不同角度给出了社区的定义[5, 17, 37] 。其中,菲利波·拉迪奇(Filippo Radicchi)[21] 等人基于节点的出度和入度提出了强社区和弱社区的概念;在维基百科中社区是指有共同文化的居住于同一区域的人群。一般来说,抽象化的社区可以从边分布的稠密程度和节点之间的相似程度两个角度定义。从边分布的稠密性看,社交网络中边分布具有极大的非均匀性,某些个体之间由于外界因素紧密连接形成社区。从节点间的相似性看,社交网络中不同节点之间具有不同的相似程度,相似程度高的个体更容易聚集在一起形成社区。事实上,这两种定义在网络拓扑本质上是一致的,两个个体越相似在网络拓扑上表现为它们之间建立连接的可能性更高,所以一组相似的个体间的边密度通常也是比较高的。因此,本文讨论的社区可以定性的定义为网络中所有节点集合的一个子集,该子集内节点之间的连接相对于与子集外其他节点之间更紧密。2.2 社区发现方法评价指标
社区发现方法的性能优劣需要评价指标对其社区划分结果进行衡量。围绕这个问题,目前有模块度、标准互信息(NormalizedMutual Information)、芮氏指标(Rand Index)、Jaccard 系数等多种评价指标[5, 38] 。在此介绍两种典型的评价指标,即模块度度量和标准互信息。
马克·纽曼(M E Newman)[9, 39] 等人提出的模块度是常用的一种社区划分质量度量,其基本思想是将划分社区后的网络与不存在社区结构的零模型进行比较。对于一个网络,模块度定义为该网络的社区内部边数与相应的零模型的社区(采用相同的社区划分)内部边数的差值占整个网络边数的比值,其定义式有多种形式。为方便描述,在此给出一种便于实际计算的形式,如下所示。
根据网络的连边情况,通过该式计算出每个社区i内部节点间的连边数量eii,以及一端与社区i中节点相连的连边数量ai,即可快速计算出模块度。对于社区结构划分未知的网络,模块度能有效度量社区结构。
标准互信息度量(NMI)是信息论中的相关性度量,由莱昂·达农(Leon Danon)[40] 等人引入并用于社区划分质量评价,能有效衡量给定社区划分结果与真实网络划分的相似程度。NMI根据定义的混合矩阵N来比较真实社区与划分的社区,N中的元素Nij表示对应的两个社区间共同的节点数量,其公式如下:
其中,CA表示真实社区的数目,CB表示发现的社区数目,Ni.表示矩阵N中第i 行元素的总和,N.j表示矩阵N中第j列元素的总和。对存在真实社区划分的网络,NMI具有较好的辨识能力,I值越大,则表明发现的社区结构划分结果越准确,当发现的社区划分与真实社区一致时,I取最大值1。3 基于局部优化的社区发现方法
如前所述,基于局部优化的社区发现方法的基本思想是基于网络的局部信息来划分社区。从不同的局部优化策略,可以将这些方法大致划分为局部扩展优化、派系过滤、标签传播以及局部边聚类优化4 类。下面分别对其典型的方法加以分析。3.1 局部扩展优化方法
基于局部扩展的方法是局部社区发现常用的一类方法。一般根据定义的社区局部度量,从给定的初始节点逐步合并引起最大的社区度量增量的近邻节点,从而进行局部扩展优化,各方法的主要差异在于对局部社区的度量不同。阿龙·克劳塞蒂(Aaron Clauset)定义了一种局部模块度,并提出了一种局部扩展优化算法[23] 。该度量仅考虑社区边界节点,测量社区边界的清晰度,其定义为社区边界节点与社区内部节点连边的数量和与社区外其他节点的连边数量的比例。该算法扩展过程持续到合聚了给定数量的节点集合或者发现整个闭合的社区结构为止。该算法简单快速,但其固定的社区规模会产生局部最优的结果,进而导致产生不合理的社区结构。针对这一问题,在相同的时间复杂度下,罗峰等人提出了一种子图度量优化的局部社区扩展算法(LWP)[24] 。与拉迪奇的弱社区定义很相似,该算法定量比较社区中节点的出度和入度。另外,罗峰等人提供了3 种启发式节点搜索方式,能一定程度解决局部最优的问题。然而该方法对不同的网络选取不同的阈值,有一定随机性。
基于局部模块度度量和子图度量的社区发现结果通常包含异常节点,即社区划分结果的召回率高而精确度低,影响整体的社区质量。针对这一问题,Chen[25] 等人提出另一种局部社区度量方法,该度量考虑了社区内部和外部的连边密度,从而有效避免了异常值的出现,且在优化过程中,采取了更细致的策略以进一步强化内部关系而弱化外部联系。但该方法对处于两个社区边界的节点仍可能出现错分。为此,Ngonmang[41] 等人通过同时合并使度量函数最大化的所有节点对该方法进行了改进,而非随机选取一个节点,相对提高了社区划分精确度。詹姆斯·巴格罗(James P Bagrow)等提出了一种基于L-壳扩展的社区发现算法[22] ,其从一个初始节点出发,逐层向外访问该节点的邻居节点,当合并的节点总度增量低于某一阈值时或不再增加时,L-壳停止扩展,其覆盖的所有节点作为一个社区。该方法对初始节点选取较敏感,当选取的初始节点处在社区中心时可以实现良好的划分,当选取的节点处在社区边界时,则会出现社区溢出的情况。
针对局部社区发现对初始节点位置敏感的问题,陈琼等提出了一种基于局部度中心节点的方法(LMD算法)[42] 。该方法首先找到与初始节点连接的局部最大度节点,再从最大度节点开始扩展社区结构,逐步通过优化局部社区度量找到社区,最后对结果进一步优化。其他一些如找到社区中的核心节点[43] 、最大派系[44] 等改进方法,先通过找到社区中的核心节点或最大派系等结构,再围绕核心节点或派系将邻域节点扩展到整个社区,社区划分的精确性得到有效提高。
基于特定节点的局部社区发现方法可扩展用于整个网络结构的社区发现和重叠结构发现。尽管以上方法能一定程度揭示网络社区结构的层次性或重叠性,但无法有效发现同时表现出层次和重叠两种特性的社区结构。针对这一问题,安德烈亚(AndreaLancichinetti)等人提出了一种随机种子节点的局部优化的方法(LFM 算法[20])。该方法定义了一种节点适应度来度量社区内部边与社区外部边的关系。基于节点适应度的贪婪优化,从一个种子节点开始逐步合并一个使社区节点适应度增加的邻居节点或删除一个使其减小的节点,直到出现适应度负值为止。不同的是,在搜索过程中,无论节点是否被分到某个社区,都可以多次被访问,使得每个节点可以包含在多个社区。同时,通过对不同分辨率参数进行调节可得到社区的层次结构。该方法相对来说较灵活可靠。由于LFM算法的种子节点的选取是随机的,可能导致不稳定的结果,康拉德·李(Conrad Lee)等对LFM算法进行了补充并提出“贪婪派系”扩展优化算法(GCE算法)[45] ,其使用最大派系作为种子,再通过局部社区适应度对这些种子进行扩展。GCE 算法使社区划分结果更加稳健,同时更有效揭示高度重叠的社区结构。3.2 派系过滤方法
派系过滤方法(CPM)最初是由杰尔杰伊·帕尔拉(Gergely Palla)等人提出用来分析重叠社区结构的有效方法[19, 32] ,其定义了一种严格的社区结构,并允许社区间存在重叠。如上所述,社区结构的重叠性普遍存在于各种社交网络中,网络中节点可以同时属于多个派系。CPM算法定义K-派系结构是网络中包含K 个节点的完全子图(K 团),所有彼此连通的K-派系的集合构成一个K-派系社区。CPM算法通过对网络中各节点的度可判断可能存在的最大派系,从一个节点出发找到包含该节点的大小为K 的派系,采用迭代回归的算法寻找网络中大小不同的派系,最后将彼此连通的K-派系集合为一个社区结构。
为进一步分析网络社区的重叠特性,伊莱什·法卡斯(Illés Farkas)等人基于子图强度将CPM算法扩展到加权网络,提出了一种加权派系过滤算法(CPMw)[46] 。该算法把子图强度有效地结合到派系搜索中,根据设定的固定强度阈值,将大于此阈值的K-派系包含到社区中。与CPM算法不同的是,CPMw算法从整体考虑派系强度,因而允许K-派系中包括低于预设阈值的边,从而得到更稳定的社区划分。
为快速找到给定大小的K-派系社区结构,并有效应用到大规模的加权和非加权社交网络,尤西·昆普拉(Jussi Kumpula)等人提出了一种快速派系过滤算法(SCP)[31] 。该算法根据边的权重递减的顺序将边添加到网络,并记录新出现的K-派系。再根据得到的K-派系结构,检测K-派系之间存在的重叠程度,以判断K-派系是否已包含在之前K-派系社区之中,逐步更新以确定最终的社区划分。SCP算法的计算复杂度与网络中K-派系数量成线性关系,其运行时间相比于CPM明显降低。该算法能有效揭示网络中社区的层次结构,另外在处理加权网络时,CPM 算法需迭代计算每个可能的权重阈值下的社区,而SCP 算法只需要运行一次就能获得多阈值下的社区结构同时嵌套的社区结构。在处理大规模加权社交网络,当缺乏有关合适阈值的先验知识或研究多阈值下社区结构时,SCP算法就显得非常有效。3.3 标签传播方法
标签传播算法(LPA算法)是一种简单高效的局部社区发现方法,由拉加万(Usha NandiniRaghavan)等人[27] 提出。该方法仅用局部的网络结构来完成社区划分,而非对特定的社区强度指标的优化。LPA算法具体过程为:首先为网络中每个节点初始化一个唯一的标签,标签根据网络局部结构信息的传播规则在网络中传播,直到所有节点的标签传播达到稳定,最后将具有相同标签的节点划分到一个社区中。在每次迭代后,每个节点标签更新为其邻居节点使用最多的标签。这个传播规则定义了网络的社区结构,即网络中每个节点选择加入的社区是它最多数量的邻居节点属于的社区。LPA 算法能有效地提取社区结构,且每次迭代的计算复杂度接近线性时间。
由于LPA算法基于单个标签传播,网络中的每个节点被确定地划分至单一社区中,因而忽略了社区结构的重叠特性。为了同时揭示在线社交网络的重叠社区结构,史蒂夫·格利高里(SteveGregory)将LPA算法扩展为多标签传播算法(COPRA算法)[30] 。该算法通过使节点同时具有多个标签,使节点同时携带多个社区信息,将LPA扩展为一般化的标签传播过程,并用一个参数来控制社区间的重叠程度。COPRA 算法在每次迭代后同步更新并计算每个节点对于不同社区标签的隶属程度,即得到每个节点的标签与所属程度的关系对。在标签迭代传播时,将每个节点的标签更新为其所有邻居标签集合,去掉低于预设阈值的标签并进行标准化处理。对于存在多个具有最大隶属系数的节点,从中随机选取一个,这种随机选取的策略使得该算法具有很大的不确定性。
虽然LPA算法时间复杂度低,且实施过程简单,但算法具有不确定性。在传播过程中,某些标签被其他标签控制而逐渐消失,导致社区数量单调减少,从而出现社区巨片。因此,兰·莱昂(IanX. Y. Leung)[29] 等人提出了改进的LPA方法。由于LPA不考虑标签的传播距离,不管标签传播多远,对其他标签更新的影响都不变,导致某个社区中的标签可以传播很远而侵入到其他社区中,形成规模巨大的社区。在改进的方法中,兰·莱昂等人为每个标签分配了一个分数,该分数随着标签传播距离的增大而降低。使用该分数对标签在传播过程中的影响力进行加权,随着标签传播距离的增大,其对其他标签更新的影响力将逐渐变小,这样可以有效地控制某个标签由于传播过远而侵入其他的社区,从而有效防止极大的社区结构的形成。3.4 局部边聚类优化方法
以边为研究对象的社区发现方法相对于传统的基于点的划分具有一定的优势[47, 48] ,而基于边聚类的局部社区发现方法能有效揭示社区的局部属性。菲利波·拉迪奇(Filippo Radicchi)等人定义了一种边聚类系数,并提出了一种社区发现的局部方法[21] 。边聚类系数反映了一条边与周围邻边连接的紧密程度,与边介数不同的是,它是一种局部度量,其定义为包含给定边的三角形数量与最大可能存在的三角形数量之比。这种三角形结构大量存在于社区内部,对属于不同社区的节点间的连边往往不存在或很少。该算法采用类似GN算法的分裂过程[49] ,逐步去除边聚类系数最小的边,以得到整个社区划分。该算法相对于GN 算法在计算速度上有显著提高,但在方法上对结果的评价存在一定的主观性。为此,西美昂·帕帕扎基斯(SymeonPapadopoulos)等人提出一种桥边界的局部社区发现方法[50] 。该算法在边聚类系数的基础上定义了一种桥边界,即一条边作为社区边界的程度。围绕一个种子节点,重复地添加邻居节点以搜索局部社区拓扑结构,直到找到社区边界的边为止。若社区中的一条边聚类系数超过预定的阈值,则这条边即为桥边界。该方法能够得到有效的局部社区,同时可以通过多点扩展用于整个网络社区发现,计算复杂度低,但其采用了固定的阈值而非自适应的策略来确定社区边界。
以上基于边聚类系数的社区发现方法忽略了社区的重叠性,因此,Ahn 等人提出了一种基于连边局部相似性的边社区发现方法来检测社区的重叠性和层次性[33] 。该方法定义社区为一组紧密相连的连边的集合,而非通常定义的节点集合。在一个有聚类层次的树图中,每个叶子表示一条边,相应的分支作为边社区。同时,在连边树图中每条边的位置是确定的,而由于一个节点可以与多条边相连,如果这些连边属于不同的社区,那么这个节点相应的属于这些不同的社区,从而有效地揭示社区的重叠性。该方法将连边对的相似度定义为两连边所共同拥有的共同邻居的相对数量,其具体过程为:首先,根据连边相似定义,计算网络中连边对的相似度,将最相似的连边逐步合并为一个边社区,得到一个层次聚类的连边树图;然后通过优化社区内部的连边密度来确定分割树图的最佳位置或合并过程结束的条件,以得到最佳的社区结构,同时,该边社区划分密度是一种局部度量,从而避免了模块度具有的分辨率限制问题[51] 。该边社区发现方法不仅能发现最大划分的社区,而且有效揭示层次化的社区结构特征。
另外,基于边聚类的思想,潘磊等人提出另一种局部的边社区发现方法[52] ,其先采用边聚类系数对网络中的边进行排序,然后选取一条值最大的初始边,根据定义的社区适应度函数由初始边开始不断地扩张邻居边加入社区,从而得到一个局部边社区结构,再还原节点得到可重叠的社区结构,而通过对整个网络迭代地使用这一过程,可以得到整个网络的社区结构。该方法对最终的社区划分结果进行进一步优化,以得到最优的重叠社区结构。类似地,吴英骏等人提出一种连接相似度的局部社区发现方法[53] ,通过度量节点与社区间连边的相似性进行聚类,得到较理想的局部社区结构。4 展望
对于社区发现的研究已历经了很长时间,取得了很多非常有价值的成果。大量的社区发现方法,从不同角度刻画了社区结构特性,加深了人们对网络结构及群体特征的理解。然而时下的社交网络呈现出大规模、强交互性、动态演化的特征,因此在处理速度、精确性及动态应对等方面对社区发现方法提出了更高要求。随着研究的深入以及相关技术的发展,目前还存在一些有待进一步研究的问题。
(1)快速是社区发现方法的基本要求和发展趋势。面对规模持续增长、交互性不断加强及群体行为不断变化的社交网络,如何运用更高效的方法和技术(如并行化处理、抽样等)来处理大规模在线数据,是社交网络分析领域共同面临的重要问题,同时是社区发现中值得深入研究的问题。
(2)精确性是社区发现技术的重要研究方向。如何找到自然意义下的真实社区结构,是所有方法试图解决的问题。关于社区结构,存在各种不同描述和定义,目前尚无统一的标准。一些定义是基于社区内部节点间联系的不同程度度量,一些依赖于所采用的理论模型和演化过程。其次,通过对基于局部扩展的各种方法的聚类过程和相关社区度量进行对比分析发现,大多数局部社区发现方法通常对起始节点的位置比较敏感,尽管已有方法提出改善这一问题,并能在一定程度上优化社区结构划分,但是还不能从根本上解决局部最优的问题。这类似于聚类中的聚类中心选取的问题。最近,一种新颖的聚类中心确定方法被提出[54] ,其将聚类中心定义为远离高密度节点的局部密度最优的节点,该方法基于相对密度而非绝对密度来确定类簇,从而有效地排除异常点。该方法能给社交网络分析中的社区挖掘研究提供一定的启发。
(3)综合的分析系统。由于网络结构的多样性和复杂性,以及应用背景的差异,目前尚无一个统一的评价标准和体系,且实际应用对社区划分的时效性和精确性的要求不断提高。不同社区发现方法在具体应用环境下各显所长,不同的评价准则对不同的网络结构表现出不同的优势,如何提高算法的可扩展性、如何将这些优势引入其他方法以及如何有机整合、合理地相互补充都是有意义的研究方向。
(4)社交网络动态演化。在社交网络中,特别是在线社交媒体中,网络结构呈现动态变化,个体及群体行为特征复杂多样,这给社区发现方法提出了更高要求,亟需更有效、更系统的方法和技术来解决。
| [1] | Jennifer G. Analyzing the social web.Waltham, MA: MorganKaufmann, 2013. |
| Click to display the text | |
| [2] | Nettleton D F. Data mining of social networks represented asgraphs. Computer Science Review, 2013, (7): 1-34. |
| Click to display the text | |
| [3] | Alan M, Massimiliano M, P GK et al. Measurement and analysisof online social networks. Proceedings of the 7th ACM SIGCOMMconference on Internet measurement: ACM, 2007,29-42. |
| Click to display the text | |
| [4] | Schaeffer S E. Graph clustering. Computer Science Review, 2007,1 (1): 27-64. |
| Click to display the text | |
| [5] | Fortunato S. Community detection in graphs. Physics Reports,2010, 486 (3-5): 75-174. |
| Click to display the text | |
| [6] | Shen H, Cheng X, Cai K et al. Detect overlapping and hierarchical community structure in networks. Physica A: Statistical Mechanicsand its Applications, 2009, 388 (8): 1706-1712. |
| Click to display the text | |
| [7] | Newman M E J. Communities, modules and large-scale structurein networks. Nature Physics, 2012, 8 (1): 25-31. |
| Click to display the text | |
| [8] | Clauset A, Newman M E, Moore C. Finding community structurein very large networks. Physical Review E, 2004, 70 (6): 066111. |
| Click to display the text | |
| [9] | Newman M E. Fast algorithm for detecting community structurein networks. Physical Review E, Statistical, Nonlinear, and SoftMatter Physics, 2004, 69 (6 Pt 2): 066133. |
| Click to display the text | |
| [10] | Muff S, Rao F, Caflisch A. Local modularity measure for networkclusterizations. Physical Review E, Statistical, Nonlinear,and Soft Matter Physics, 2005, 72 (5 Pt 2): 056107. |
| Click to display the text | |
| [11] | Newman M E. Modularity and community structure in networks.Proceedings of the National Academy of Sciences of the UnitedStates of America, 2006, 103 (23):8577-8582. |
| Click to display the text | |
| [12] | Blondel V D, Guillaume J L, Lambiotte R et al. Fast unfolding ofcommunities in large networks. Journal of Statistical Mechanics:Theory and Experiment, 2008, 2008 (10): P10008. |
| Click to display the text | |
| [13] | Lancichinetti A, Fortunato S. Limits of modularity maximizationin community detection. Physical Review E, Statistical, Nonlinear,and Soft Matter Physics, 2011, 84 (6 Pt 2): 066122. |
| Click to display the text | |
| [14] | Sun P G, Gao L, Yang Y. Maximizing modularity intensity forcommunity partition and evolution. Information Sciences, 2013,236:83-92. |
| Click to display the text | |
| [15] | Nascimento M C V, de Carvalho ACPLF. Spectral methods forgraph clustering - A survey. European Journal of Operational Research,2011, 211 (2): 221-231. |
| Click to display the text | |
| [16] | Donetti L, Mu?oz MA. Detecting network communities: a newsystematic and efficient algorithm. Journal of Statistical Mechanics:Theory and Experiment, 2004, 2004 (10): P10012. |
| Click to display the text | |
| [17] | Papadopoulos S, Kompatsiaris Y, Vakali A et al. Communitydetection in social media. Data Mining and KnowledgeDiscovery, 2011, 24 (3): 515-54. |
| Click to display the text | |
| [18] | Dongen V, Marinus S. Graph clustering by flow simulation.Utrecht: Dutch National Research Institute forMathematics and Computer Science, 2000. |
| Click to display the text | |
| [19] | Palla G, Derenyi I, Farkas I et al. Uncovering the overlappingcommunity structure of complex networks in natureand society. Nature, 2005, 435 (7043): 814-8. |
| Click to display the text | |
| [20] | Lancichinetti A, Fortunato S, Kertész J. Detecting theoverlapping and hierarchical community structure incomplex networks. New Journal of Physics, 2009, 11 (3): 033015. |
| Click to display the text | |
| [21] | Radicchi F, Castellano C, Cecconi F et al. Defining andidentifying communities in networks. Proceedings of theNational Academy of Sciences of the United States ofAmerica, 2004, 101 (9): 2658-2663. |
| Click to display the text | |
| [22] | Bagrow J P, Bollt E M. Local method for detecting communities.Physical Review E, Statistical, Nonlinear, andSoft Matter Physics, 2005, 72 (4 Pt 2): 046108. |
| Click to display the text | |
| [23] | Clauset A. Finding local community structure in networks.Physical Review E, 2005, 72 (2):026132. |
| Click to display the text | |
| [24] | Luo F,Wang J Z, Promislow E. Exploring local communitystructures in large networks.Web Intelligence andAgent Systems, 2008, 6 (4): 387-400. |
| [25] | Chen J, Za?ane O, Goebel R. Local community identificationin social networks. Social Network Analysis andMining, 2009 ASONAM'09 International Conference onAdvances in: IEEE, 2009, 237-242. |
| Click to display the text | |
| [26] | Raghavan U N, Albert R, Kumara S. Near linear time algorithmto detect community structures in large-scale networks.Physical Review E, 2007, 76 (3): 036106. |
| Click to display the text | |
| [27] | Raghavan U N, Albert R, Kumara S. Near linear time algorithmto detect community structures in large-scale networks.Physical Review E, Statistical, Nonlinear, andSoft Matter Physics, 2007, 76 (3 Pt 2): 036106. |
| Click to display the text | |
| [28] | Barber M J, Clark JW. Detecting network communitiesby propagating labels under constraints. Physical ReviewE, 2009, 80 (2): 026129. |
| Click to display the text | |
| [29] | Leung I X, Hui P, Lio P et al. Crowcroft J. Towards real-time community detection in large networks. PhysicalReview E, 2009, 79 (6): 066107. |
| Click to display the text | |
| [30] | Gregory S. Finding overlapping communities in networksby label propagation. New Journal of Physics,2010, 12 (10): 103018. |
| Click to display the text | |
| [31] | Kumpula J M, Kivela M, Kaski K et al. Sequential algorithmfor fast clique percolation. Physical Review E, Statistical,Nonlinear, and Soft Matter Physics, 2008, 78 (2Pt 2): 026109. |
| Click to display the text | |
| [32] | Derényi I, Palla G, Vicsek T. Clique percolation in randomnetworks. Physical Review Letters, 2005, 94 (16): 160202. |
| Click to display the text | |
| [33] | Ahn YY, Bagrow J P, Lehmann S. Link communities revealmultiscale complexity in networks. Nature, 2010,466 (7307): 761-764. |
| Click to display the text | |
| [34] | Leskovec J, Lang K J, Dasgupta A et al. Communitystructure in large networks: Natural cluster sizes and theabsence of large well-defined clusters. Internet Mathematics,2009, 6 (1): 29-123. |
| Click to display the text | |
| [35] | Bagrow J P. Evaluating local community methods in networks.Journal of Statistical Mechanics: Theory and Experiment,2008,2008 (05): P05001. |
| Click to display the text | |
| [36] | Huang J, Sun H, Liu Y et al. Towards online multiresolutioncommunity detection in large-scale networks. PloSone, 2011, 6 (8): e23829. |
| Click to display the text | |
| [37] | Porter MA, Onnela J P, Mucha PJ. Communities in networks.Notices of the AMS, 2009, 56 (9): 1082-1097. |
| Click to display the text | |
| [38] | RandWM. Objective criteria for the evaluation of clusteringmethods. Journal of the American Statistical association,1971, 66 (336): 846-850. |
| Click to display the text | |
| [39] | Newman M E, Girvan M. Finding and evaluating communitystructure in networks. Physical Review E, Statistical,Nonlinear, and Soft Matter Physics, 2004, 69 (2 Pt2): 026113. |
| Click to display the text | |
| [40] | Danon L, Diaz-Guilera A, Duch J et al. Comparing communitystructure identification. J Stat Mech-Theory E, 2005. |
| Click to display the text | |
| [41] | Ngonmang B, Tchuente M, Viennet E. Local community identificationin social networks. Parallel Processing Letters, 2012, 22 (01). |
| Click to display the text | |
| [42] | Chen Q,Wu T T, Fang M. Detecting local community structuresin complex networks based on local degree central nodes. Physicaa-Statistical Mechanics And Its Applications, 2013, 392 (3): 529-37. |
| Click to display the text | |
| [43] | Zhang T T,Wu B. A Method for Local Community Detection byFinding Core Nodes. 2012 IEEE/ACM international conferenceon advances in social networks analysis and mining (asonam),2012,1171-1176. |
| Click to display the text | |
| [44] | Fanrong M, Mu Z, Yong Z et al. Local community detection incomplex networks based on maximum cliques extension. MathProbl Eng, 2014, 2014:1-12. |
| Click to display the text | |
| [45] | Lee C, Reid F, McDaid A et al. Detecting highly overlapping communitystructure by greedy clique expansion. arXiv preprint arXiv:10021827, 2010. |
| Click to display the text | |
| [46] | Farkas I, ábel D, Palla G et al.Weighted network modules. NewJournal of Physics, 2007, 9 (6): 180. |
| Click to display the text | |
| [47] | Evans T, Lambiotte R. Line graphs, link partitions, and overlappingcommunities. Physical Review E, 2009, 80 (1): 016105. |
| Click to display the text | |
| [48] | Kim Y, Jeong H. Map equation for link communities. Physical ReviewE, 2011, 84 (2): 026110. |
| Click to display the text | |
| [49] | Girvan M, Newman M E. Community structure in social and biologicalnetworks. Proceedings of the National Academy of Sciencesof the United States of America, 2002, 99 (12):7821-7826. |
| Click to display the text | |
| [50] | Symeon Papadopoulos AS, Athena Vakali, Yiannis Kompatsiariset al. Bridge bounding: A local approach for efficient communitydiscovery in complex networks. Physics and Society, 2009. |
| Click to display the text | |
| [51] | Fortunato S, Barthelemy M. Resolution limit in community detection.Proceedings of the National Academy of Sciences of theUnited States of America, 2007, 104 (1): 36-41. |
| Click to display the text | |
| [52] | Pan L, Jin J,Wang C et al. Detecting Link Communities Based onLocal Information in Social Networks. Acta Electronica Sinica,2012, 40 (11): 2255-2263. |
| [53] | Wu Y J, Huang H, Hao Z F et al. Local community detection usinglink similarity. J Comput Sci Tech-Ch, 2012, 27 (6): 1261-1268. |
| Click to display the text | |
| [54] | Rodriguez A, Laio A. Clustering by fast search and find of densitypeaks. Science, 2014, 344 (6191): 1492-1496. |
| Click to display the text |