2. 中国科学技术大学 合肥 230026
2. University of Science and Technology of China, Hefei 230026, China
“墨子号”量子科学实验卫星是中科院空间科学战略性先导科技专项中首批确定的 5 颗科学实验卫星之一,该项目目标为建立卫星与地面远距离量子科学实验平台,并在此平台上完成空间大尺度量子科学实验,以期取得量子力学基础物理研究重大突破和一系列具有国际显示度的科学成果。
量子通信基于量子物理学的基本原理,克服了经典加密技术内在的安全隐患,是迄今为止唯一被严格证明是无条件安全的通信方式,可以从根本上解决国防、金融、政务、商业等领域的信息安全问题。目前,基于光纤的城域和城际量子通信技术正在走向实用化和产业化,我国在这方面已经走在了世界前列。但是由于光纤的固有损耗以及单光子状态的不可复制性,目前点对点光纤量子通信的距离难以突破百公里量级。因此,要实现广域乃至全球化的量子通信网络,还需要借助卫星的中转。
因此,从 2003 年起,中国科学技术大学潘建伟团队率先开展远距离自由空间量子通信实验研究。2004 年底,潘建伟团队实现了 13 公里自由空间的量子纠缠分发和量子密钥分发,在国际上首次证实了光子纠缠态在穿透大气层后,其量子性质仍然能有效保持,验证了星地量子通信的可行性[1]。此后,在“远距离量子通信实验研究”和“空间尺度量子实验关键技术与验证”两个中科院知识创新工程重大项目的支持下,潘建伟团队联合中科院上海技术物理所、中科院微小卫星工程中心等单位,开展了一系列关键技术突破与地面验证实验,先后实现了16 公里自由空间量子隐形传态[2]、100 公里级自由空间量子隐形传态和双向量子纠缠分发[3]、星地量子通信的全方位地基验证[4]等重要实验,为实现星地量子通信奠定了坚实的科学与技术基础。
在完成上述系列关键技术突破的基础上,2011 年底,由中国科学技术大学牵头提出并策划的中科院战略性先导科技专项“量子科学实验卫星”正式立项。量子科学实验卫星建设和研制任务包括卫星系统、运载火箭系统、发射场系统、地面支撑系统、测控系统和科学应用系统六大系统。中国科学技术大学牵头负责确立整个专项的科学研究目标、总体技术目标和总体实验基本方案,负责科学应用系统的研制,并与中科院上海技术物理所合作完成有效载荷研制,包括负责研制量子纠缠源、量子实验控制与处理机,参与研制量子密钥通信机、量子纠缠发射机;上海微小卫星工程中心负责卫星平台研制;中科院国家天文台和中科院光电技术院负责量子通信地面站的建设。量子科学实验卫星突破了包括同时瞄准两个地面站的高精度星地光路对准、星地偏振态保持与基矢校正、星载量子纠缠源等一系列关键工程技术。
“墨子号”重量约 640 公斤,设计寿命为两年,运行在高度约 500 公里的极地轨道。目前,“墨子号”已进入预定轨道,开始为期约 3 个月的在轨测试。星地量子信道已经建立,如图 1 所示,地点为国家天文台兴隆观测站。所有测试完成后,将在首席科学家的领导下,由科学应用系统组织完成星地高速量子密钥分发、广域量子通信网络、星地量子纠缠分发以及地星量子隐形传态等多项科学实验任务,实现专项预定的科学目标:

|
| 图 1 建立星地量子链路( 红色为是地面信标光,绿色为是星上信标光) |
(1) 进行星地高速量子密钥分发实验,并在此基础上进行广域量子密钥网络实验,以期在空间量子保密通信实用化方面取得重大突破;
(2) 在空间尺度进行量子纠缠分发和量子隐形传态实验,开展空间尺度量子力学完备性检验的实验研究。
1 高速量子密钥分发及广域量子密钥网络实验量子密钥分发(Quantum key distribution)克服了经典加密技术内在的安全隐患,是迄今唯一被严格证明是无条件安全的通信方式,可以从根本上解决国防、金融、政务、能源、商业等领域的信息安全问题。量子密钥分发起源于 1984 年 IBM 实验室的 Bennett 和加拿大蒙特利尔大学的 Brassard 共同提出的量子密钥分发协议,即著名的 BB84 协议[5]。该协议基于单个光量子不可分割和量子不可克隆原理,发送方和接收方采用单光子的状态作为信息载体来建立密钥。窃听者不能分割和复制单光子,只能截取单光子后测量其状态,然后根据测量结果发送一个相同状态的光子给接收方,以期窃听行为不被察觉。但由于窃听者的测量行为会对光子的状态产生扰动,其发送给接收方的光子的状态与其原始状态会存在偏差,发送方和接收方可以利用这个偏差探测到窃听行为,因而保证了量子密钥分发的无条件安全性。Shor、Preskill[6]、Lutkenhaus[7]和 Mayer[8]等人先后独立地证明了使用理想单光子源的 BB84 协议是安全的,并在考虑窃听、噪声、非理想单光子源等条件的情况下,给出了量子密码的安全成码效率公式。
1991 年,Bennett 等在 32 厘米的距离上演示了首个量子密钥分发[9]。1995 年,中科院物理所吴令安小组在实验室内完成了我国最早的量子密钥分发实验演示[10]。2000 年,该小组又与中科院研究生院合作利用单模光纤完成了 1.1 公里的量子密钥分发演示实验[11]。2002—2003年间,瑞士日内瓦大学 Gisin 小组和我国华东师范大学曾和平小组分别在 67 公里和 50 公里光纤中演示了量子密钥分发[12, 13]。2004年,英国剑桥大学 Shields 小组和日本 NEC 公司分别实现了122 公里和 150 公里的光纤量子密钥分发演示性实验[14, 15]。2005 年,中国科学技术大学郭光灿小组在北京和天津之间也实现了125 公里光纤的量子密钥分发演示性实验。截至 2005 年,国际上已有 3 个实验小组声称可将量子通信距离达到 100 公里以上。
然而,由于理想单光子源的实用化一直没有满意的结果,在理想单光子源缺乏的情况下,利用弱相干光源成为一种方便的选择。但由于弱相干光源中存在多光子事件,如同 Brassard 所指出的,这存在所谓“分离光子数”攻击,即窃听者将单光子事件完全阻隔,而将多光子事件保留并从中截取一个光子来获得密钥信息[16]。根据理论推算,这些演示实际上在光纤长度超过 10 公里时已经不安全了。这严重影响了量子密钥分发技术的实用化。
2005 年,华人科学家王向斌、罗开广、马雄峰和陈凯等提出了经过严格理论分析的诱骗态方案[17, 18],使用弱相干激光光源就可以得到和理想单光子源几乎一样的安全性和效率。2007 年,中国科学技术大学潘建伟小组利用诱骗态方案,在国际上首次将光纤量子通信的安全距离突破 100 公里,打开了量子密钥分发技术实用化的大门[19]。在此基础上,潘建伟团队在 2008 年和 2009 年先后实现了国际上首个光量子电话网和全通型城域量子通信网络[20, 21]。2009年,潘建伟团队又在世界上率先将诱骗态方案量子密钥分发的安全距离突破至 200 公里[22]。
伴随着地面光纤网络的建成,还需要通过卫星实现星地之间的量子密钥分发,从而满足更远距离的量子保密通信需求。基于卫星等航天器的空间量子通信有着地面光纤量子通信网络无法比拟的优势。第一个原因是在同样距离下,光子在光纤中的损耗远高于自由空间的损耗。光子在自由空间的损耗主要来自光斑的发散、大气对光子的吸收和散射,远小于光纤;第二个原因是受到地面条件的限制,很多地方无法铺设量子通信的专用光纤。因此要建设覆盖全球的量子通信网络,必需依赖卫星的中转。
“墨子号”量子科学实验卫星设置了星地高速量子密钥分发科学实验任务,即在高精度捕获、跟踪、瞄准系统的辅助下,建立地面与卫星之间超远距离的量子信道,实现卫星与地面之间的诱骗态量子密钥分发,开展无条件安全的星地量子保密通信实验,量子密钥初始码产生率约为 10kbps,为建立全球范围的量子通信网络打下技术基础(图 2)。
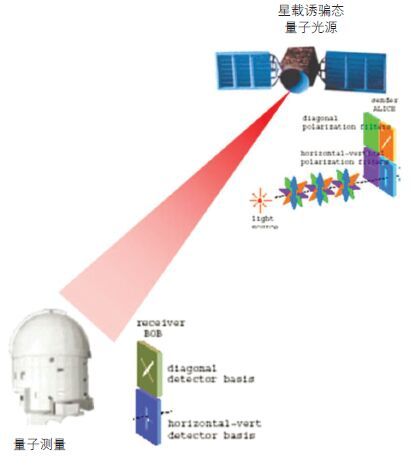
|
| 图 2 星地量子密钥分发示意图 |
“墨子”号量子科学实验卫星将在实现高速星地量子密钥分发的基础上,与两个光学地面站及其附属的两个局域光纤量子通信网络相结合,通过卫星中转的方式组建真正意义上的广域量子通信网络(图 3)。
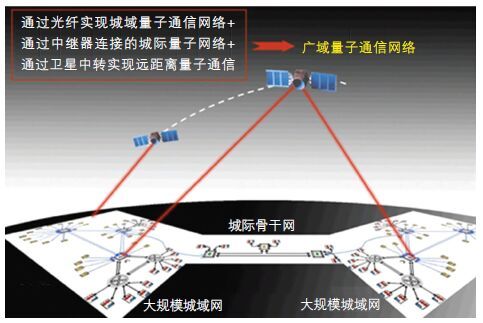
|
| 图 3 广域量子通信路线图 |
“量子纠缠”是一种多体量子叠加态。以双粒子为例,一个粒子 A 可以处于叠加态,可以用一个量子比特来表示,即 ψA = α | 0〉A+ β | 1〉A,其中 | 〉 为狄拉克符号,代表量子态。α 和 β 是任意两个复数,满足关系|α|2+|β|2=1。当两个粒子(A 和 B)发生纠缠,就会形成一个双粒子的叠加态:ψAB = α | 0〉A| 1〉B+ β | 1〉A| 0〉B,这就是一个纠缠态。对这两个粒子进行{| 0〉,| 1〉}基的测量,当 A 粒子的测量结果是 | 0〉 时,B 粒子的一定测量结果是| 1〉;反之,当 A 粒子的测量结果是 | 1〉时,B 粒子的一定测量结果是 | 0〉。这种 AB 粒子之间的状态关联是非局域的,即使对 AB 的测量是在类空间隔进行,也会得到同样的结果,这就是量子力学的非定域性。
量子纠缠得到重视始于爱因斯坦对量子力学的批评,他认为量子力学是不完备的,不符合自己根据相对论提出的“局域实在原理”(Local realism):(1)物质实体独立于任何测量而存在;(2)物质之间的任何影响都是时空局域的,即不能超过光速。
1935 年,爱因斯坦和波多尔斯基(Podolsky)、罗森(Rosen)一同提出了著名的 EPR(Einstein-Podolsky-Rosen)佯谬[23],用来论证量子力学的不完备性:根据海森堡的不确定关系,无法同时测量一个粒子的位置和动量的精确值。于是 EPR 佯谬设想两个相互作用的粒子 A 和 B,总动量确定(即一个 EPR 对)。当两个粒子分隔距离很远时,测量 A 的位置可得到精确值;同时测量 B 的动量也可得到精确值,从而计算出 A 的动量的精确值,这就同时精确测量了 A 的位置和动量,违反了不确定关系。这种跨越空间的瞬间影响双方的量子纠缠曾经被爱因斯坦称为“鬼魅的超距作用”(spooky action at a distance)
但量子力学中不是这样。因为粒子 A 和 B 处于“纠缠态”,当精确测量 A 的位置时,影响到了 B,使 B 的动量无法精确测量,反之亦然。因为两个粒子已经相距很远并且无相互作用,于是 EPR 文章中认为量子纠缠暗示了:(1)要么这两个粒子存在某种超过光速的非局域(Non-locality)相互作用而违背相对论;(2)要么量子力学的描述是不完备的,存在未知的“隐变量”来抵消这种非局域相互作用,使 A 和 B 依然符合定域实在原理。
1964 年爱尔兰物理学家贝尔推导出一个不等式,可用来判定量子力学和隐变量理论谁正确[24]。如果实验结果符合贝尔不等式,则隐变量理论胜出;如果实验结果违反了贝尔不等式,则量子力学胜出。20 世纪 80 年代 John Clauser、Stuart Freedman 和 Alain Aspect 等人的一系列实验证实了量子纠缠的确违反贝尔不等式[25-27],从而否定了局域隐变量的存在。后来的几次检验贝尔不等式的实验都证实量子纠缠是非定域的,因此爱因斯坦的定域性原理需要舍弃。2015 年荷兰代尔夫特大学的 Hanson 研究组实现了同时关闭探测效率漏洞和局域性漏洞的贝尔不等式检验,进一步验证了量子非定域性[27]。
而要实现对量子非定域性的终极检验,诺贝尔物理学奖获得者 Anthony Leggett 指出,还需要引入人的自由意志来彻底杜绝可能存在于各种仪器中的隐变量,这就需要在人的反应时间内来进行类空间隔的贝尔不等式检验,量子纠缠的分发要达到数十万公里的距离。这样遥远的距离就必须要求在外太空进行。同时,量子纠缠是否会受到引力的影响,仍然需要进一步的验证。
“墨子号”量子科学实验卫星将量子纠缠光源放置于卫星平台上,同时向两个相距千公里的地面站进行双向量子纠缠分发。在完成量子纠缠分发后,对纠缠光子同时进行独立的量子测量,检验纠缠态在星地大尺度下的纠缠特性,即在世界上首次开展空间尺度量子力学非定域性(即贝尔不等式检验)的实验研究,并为未来实现引入自由意志的量子非定域性终极检验奠定技术基础。
3 地星量子隐形传态实验量子隐形传态(Quantum teleportation),是在量子纠缠的辅助下,将粒子的未知量子态传送到遥远的距离,而不用传送这个粒子本身[29, 30]。因为量子计算需要直接处理量子比特,于是“量子隐形传态”这种直接传的量子比特传输将成为未来量子计算之间的量子通信方式,多体[31]、多终端[32]、多自由度[33]的量子隐形传态是构建分布式量子信息处理网络的基本单元。
量子隐形传态的过程一般分如下 4 步。
(1)制备一个纠缠粒子对,将粒子1发射到 A 点,粒子 2 发送至 B 点(图 4)。
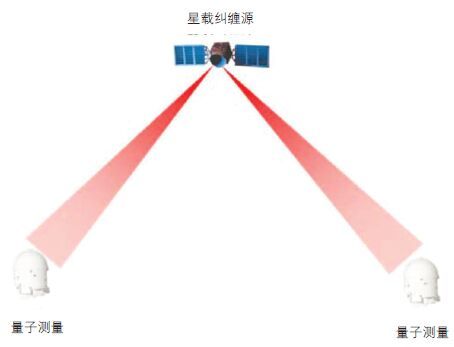
|
| 图 4 星地量子纠缠分发原理图 |
(2)在 A 点,另一个粒子 3 携带一个想要传输的量子比特 Q。于是 A 点的粒子 1 和 B 点的粒子 2 与粒子 3 一起形成一个总的态。在 A 点同时测量粒子 1 和粒子 3,得到一个测量结果。这个测量会使粒子 1 和粒子 2 的纠缠态坍缩掉,但同时粒子 1 和粒子 3 却纠缠到了一起。
(3)A 点的一方利用经典信道(就是经典通信方式,如电话等)把自己的测量结果告诉 B 点一方。
(4)B 点的一方收到 A 点的测量结果后,就知道了B 点的粒子 2 处于哪个态。只要对粒子 2 稍做一个简单的操作,它就会变成粒子 3 在测量前的状态。也就是粒子 3携带的量子比特无损地从 A 点传输到了 B 点,而粒子 3 本身只留在 A 点,并没有到 B 点(图 5)。
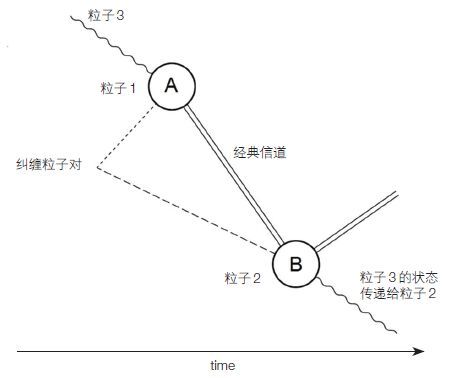
|
| 图 5 量子隐形传态过程示意图 |
以上就是通过量子纠缠实现量子隐形传态的方法,即通过量子纠缠把一个量子比特无损地从一个地点传到另一个地点。需要注意的是,由于步骤(3)是经典信息传输而且不可忽略,因此它限制了整个量子隐形传态的速度,使得量子隐形传态的信息传输速度无法超过光速。
“墨子号”量子科学实验卫星将通过在地面建立高品质量子纠缠光源,将其中一个光子通过地面发射望远镜发送到卫星平台,在地面将剩余纠缠态与待传送态进行联合纠缠测量,卫星载荷对纠缠光子进行量子测量,从而将地面的某个量子态通过隐形传态的过程传递到卫星平台上,实现基于光子纠缠的地星量子隐形传态实验(图 6)。
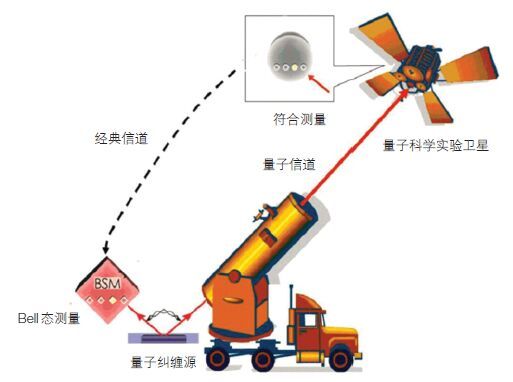
|
| 图 6 地星量子隐形传态实验示意图 |
“墨子号”量子科学实验卫星的成功研制和发射使得中国进一步扩大了在量子通信领域国际领先的优势。在实现一系列空间尺度量子科学实验目标的同时,在量子通信技术实用化上致力于实现国家信息安全和信息技术水平跨越式提升。另一方面,2016 年底,由中国科学技术大学牵头承担的国家发改委“京沪干线”广域量子通信骨干网络工程也将建成并全线开通。京沪干线将建成连接北京、上海,贯穿济南、合肥等地,全长约 2 000公里的大尺度量子通信技术验证、应用研究和应用示范平台。结合量子科学实验卫星和京沪干线,将初步构建我国天地一体化的广域量子通信网络基础设施,推动量子通信技术的深入应用、形成战略性新兴产业。
“墨子号”还将首次在空间尺度上实现对量子力学非定域性的实验检验,加深人类对量子力学基本原理的理解,并为量子力学非定域性的终极检验奠定基础。空间量子科学实验平台的建立,还将为探索和检验广义相对论、量子引力等物理学基本原理提供全新的手段。
| [1] | Peng C Z, Yang T, Bao X H, et al. Experimental free-space distribution of entangled photon pairs over 13 km:towards satellite-based global quantum communication. Physical Review Letters , 2005, 94 (15) : 4. |
| [2] | J in, X M, Ren J G, Yang B, et al. Experimental free-space quantum teleportation. Nature Photonics , 2010, 4 (6) : 376–381. DOI:10.1038/nphoton.2010.87 |
| [3] | Yin J, Ren J G, Lu H, et al. Quantum teleportation and entanglement distribution over 100-kilometre free-space channels. Nature , 2012, 488 (7410) : 185–188. DOI:10.1038/nature11332 |
| [4] | Wang J Y, Yang B, Liao S K, et al. Direct and full-scale experimental verifications towards ground-satellite quantum key distribution. Nature Photonics , 2013, 7 (5) : 387–393. DOI:10.1038/nphoton.2013.89 |
| [5] | Bennett C H, Brassard G. Quantum cryptography:Public key distribution and coin tossing. In Proceedings of IEEE International Conference on Computers, Systems and Signal Processing. 1984, 175:8-11. |
| [6] | Shor P W, Preskill J. Simple proof of security of the BB84 quantum key distribution protocol. Physical Review Letters , 2000, 85 (2) : 441–444. DOI:10.1103/PhysRevLett.85.441 |
| [7] | Lutkenhaus N. Dim, coherent states as signal states in the BB84 protocol:Is it secure? Quantum Communication, Computing, and Measurement 2, 2000, 387-392. |
| [8] | Mayers D. Unconditional security in quantum cryptography. Journal of the ACM , 2001, 48 (3) : 351–406. DOI:10.1145/382780.382781 |
| [9] | Charles H B, François B, Gilles B, et al. Experimental quantum cryptography. Journal of Cryptology , 1992, 5 (1) : 3–28. |
| [10] | 邵进, 吴令安. 量子光学. 上海: 华东师范大学出版社, 1995 : 1-41. |
| [11] | 梁创, 符东浩, 梁冰, 等. 850nm光纤中1.1km量子密钥分发实验. 物理学报 , 2001, 50 (8) : 1429–1433. |
| [12] | Stucki D, Gisin N, Guinnard O, et al. Quantum key distribution over 67 km with a plug & play system. New Journal of Physics , 2002, 4 (41) : 1–8. |
| [13] | 周春源, 吴光, 陈修亮, 等. 50km光纤中量子保密通信. 中国科学 , 2003, 33 (6) : 538–543. |
| [14] | Gobby C, Yuan Z L, Shields A J. Quantum Key Distribution Over 122 km of Standard Telecom Fiber. Applied Physics Letters , 2004, 84 : 3762–3764. DOI:10.1063/1.1738173 |
| [15] | Kimura T, Nambu Y, Hatanaka T, et al. Single-photon interference over 150 km transmission using silica-based integrated-optic interferometers for quantum cryptography. Japanese Journal of Applied Physics , 2004, 43 (9) : 1217–1219. |
| [16] | Brassard G, Lutkenhaus N, Mor T. Limitations on practical quantum cryptography. Physical Review Letters , 2000, 85 (6) : 1330–1333. DOI:10.1103/PhysRevLett.85.1330 |
| [17] | Wang X B. Beating the photon-number-splitting attack in practical quantum cryptography. Physical Review Letters , 2005, 94 (23) : 230503. DOI:10.1103/PhysRevLett.94.230503 |
| [18] | Lo H K, Ma X, Chen K. Decoy state quantum key distribution. Physical Review Letters , 2005, 94 (23) : 230504. DOI:10.1103/PhysRevLett.94.230504 |
| [19] | Peng C Z, Zhang J, Yang D, et al. Experimental long-distance decoy-state quantum key distribution based on polarization encoding. Physical Review Letters , 2007, 98 (1) : 010505. DOI:10.1103/PhysRevLett.98.010505 |
| [20] | Chen T Y, Liu Y, Cai W Q, et al. Field test of a practical secure communication network with decoy-state quantum cryptography. Optics Express , 2009, 17 (8) : 6540–6549. DOI:10.1364/OE.17.006540 |
| [21] | Chen T Y, Wang J, Liang H, et al. Metropolitan all-pass and inter-city quantum communication network. Optics Express , 2010, 18 (26) : 27217–27225. DOI:10.1364/OE.18.027217 |
| [22] | Liu Y, Chen T Y, Wang J, et al. Decoy-state quantum key distribution with polarized photons over 200 km. Optics Express , 2010, 18 (8) : 8587–8594. DOI:10.1364/OE.18.008587 |
| [23] | Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete?. Physical Review , 1935, 47 (10) : 777–780. DOI:10.1103/PhysRev.47.777 |
| [24] | Bell J S. On the einstein-podolsky-rosen paradox. Physics , 1964, 1 : 195–200. |
| [25] | Freedman S J, Clauser J F. Experimental test of local hiddenvariable theories. Physical Review Letters , 1972, 28 : 938–941. DOI:10.1103/PhysRevLett.28.938 |
| [26] | Aspect A, Grangier P, Roger G. Experimental tests of realistic local theories via bell's theorem. Physical Review Letters , 1981, 47 (7) : 460–463. DOI:10.1103/PhysRevLett.47.460 |
| [27] | Weihs G, Jennewein T, Simon C, et al. Violation of Bell's inequality under strict Einstein locality conditions. Physical Review Letters , 1998, 81 : 5039–5043. DOI:10.1103/PhysRevLett.81.5039 |
| [28] | Hensen B, Bernien H, Dréau A E, et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature , 2015, 526 : 682–686. DOI:10.1038/nature15759 |
| [29] | Bennett C, Brassard G, Crépeau C, et al. Teleporting an unknown quantum state via dual classic and Einstein-Podolsky-Rosen channels. Physical Review Letters , 1993, 70 : 1895–1899. DOI:10.1103/PhysRevLett.70.1895 |
| [30] | Bouwmeester D, Pan J W, Mattle K, et al. Experimental quantum teleportation. Nature , 1997, 390 (6660) : 575–579. DOI:10.1038/37539 |
| [31] | Zhang Q, Goebel A, Wagenknecht C, et al. Experimental quantum teleportation of a two-qubit composite system. Nature Physics , 2006, 2 (10) : 678–682. DOI:10.1038/nphys417 |
| [32] | Zhao Z, Chen Y A, Zhang A N, et al. Experimental demonstration of five-photon entanglement and open-destination quantum teleportation. Nature , 2004, 430 (6995) : 54–58. DOI:10.1038/nature02643 |
| [33] | Wang X L, Cai X D, Su Z E, et al. Quantum teleportation of multiple degrees of freedom of a single photon. Nature , 2015, 518 (7540) : 516–519. DOI:10.1038/nature14246 |




