计算概念具有丰富的内涵,但由于概念体系不完善导致的名实之间的矛盾,在日常交流中计算概念内涵的丰富性往往不能被准确全面地反映。计算概念看似简单,实则不然。计算不只是指加减乘除;进一步说,计算也不只是指数值计算;更进一步说,计算也不仅仅是指数学。究竟什么是计算,计算概念具有哪些方面,这些方面之间具有怎样的关系,这些问题似乎比较基本,但答案并非显而易见。计算概念包括数学理论、机械装置、电气装置等方面,具有计算理论、计算技术、计算机器等不同内容,涉及中国古代数学的算法、西方数学的形式推理等。准确理解计算概念,需要涉及包括数学、物理学在内的整个科学体系的深层次的核心内容,需要正确把握科学与艺术、机械与巧思、几何与代数、人脑与电脑、人类智能与人工智能、工艺基础与上层建筑、证明与计算[1]、功能与性能等一系列范畴对之间的关系。
计算概念因为计算技术本身具有深刻、普遍的影响力而在社会生活和科学研究中被高频使用,因此计算概念的准确性、完备性十分重要,但目前仍存在较多问题:算力和算法是经常被使用的概念,但实际上算力本身的定义不清晰——算力是指计算机系统峰值计算能力,还是某个应用的计算能力?假如是指计算机系统峰值计算能力,那么是指哪一指令类型的计算能力?算力是否受算法的影响?算术和算法的联系和区别是什么?相对经典计算来说,量子计算提升了计算的哪个方面?如何以统一的视角看待经典计算和量子计算?在计算概念中,如何体现作为计算机系统设计者的人的作用?诸如此类的问题很重要,但使用目前的计算概念很难清楚地回答,原因除了应用程序千变万化、计算机指令集中指令类型丰富多样、计算能力是关于多个因素的多元函数等客观因素,还包括计算概念体系尚不完善。长期以来,我们对西方主导的计算概念采取了“拿来主义”的做法,并没有及时对现有计算概念进行审视、梳理、重构和补遗。本文将吸收、借鉴和应用我国古代思想,基于中国传统思想文化对计算概念进行对应与分类,提出计算概念谱系。
1 自主计算技术的重要性计算机作为一种重要的生产工具,是第3次科技革命的重要代表,对社会发展具有极大的影响力。生产力是人类社会发展的最根本的决定性因素,生产工具是生产力发展水平的标志。地球的历史约45亿年,人类的历史约几百万年,文字的历史约几千年,而代表现代计算的计算机历史仅有70多年,所以现代计算的历史是短暂的;但是,计算技术在这短暂的时间内产生的影响力是巨大的,计算技术代表的人类文明的高度是空前的。在本文中,我们将会看到我国第一届国家自然科学奖一等奖的3位得主(钱学森、华罗庚、吴文俊)都对计算发表了自己的真知灼见,都分别作出了卓越贡献。钱学森在1957年论述了如何构思算法[2],华罗庚在1956年主持筹备创建了中国科学院计算技术研究所,吴文俊在1976年发现几何定理的机械化证明方法[3],3位大师的重视无疑体现出计算的重要性。
我国计算技术领域工作者长期致力于自主掌握最先进的计算技术。世界上第一台存储程序式通用电子计算机(EDVAC)于1946年在美国宾夕法尼亚大学由冯· 诺伊曼等人研制。作为“四项紧急措施”之一,中国科学院计算技术研究所于1956年成立,并于1958年研制出中国第1台数字电子计算机。我国计算机在肇始阶段,由于工业基础薄弱,面临缺少技术资料、电子器件、人才储备的困境,而且整个软硬件体系和生态也都需要从零建构。尽管如此,我国计算机在总体设计、逻辑设计、工程设计和可靠性设计中仍然做到了较大的自主性。在体系建构之后,我国国产计算机研发过程中经历了体制变革、西方压制等内外部挑战,进入时有曲折的发展轨道。国产计算机从1960年运算速度150次每秒,到1973年达到了100万次每秒,再是2008年达到100万亿次每秒,现在已超过10亿亿次每秒。
在芯片、核心软件等成为“卡脖子”技术的时代背景下,我国在计算技术领域需要建立一种理性、坚定、辩证、实用的文化自信。这种自信建立在事实考证和真理论证基础上:不是盲目的,而是理性的、实事求是的;不是徘徊动摇的,而是坚定不移的;不是极端的,而是辩证的;不是空洞无用的,而是切实有用的。这种自信不仅仅是一种心理状态,还是一种影响科学研究目的与路径的思维和方法,关系到回答“为什么做研究”“做什么样的研究”“怎样做研究”等基本问题。中国当代学生从小学到大学的数学学习主要以西方数学内容为主,包括欧几里得创立的公理化几何学、牛顿-莱布尼茨创立的微积分等。对于中国古代的数学内容及其蕴含的思想文化,中国当代学生则继承较少。我们需要深化中华文明探源工程,夯实理性且坚定的文化自信的史实基础。我国近代科技发展滞后,在新中国建立之后,我们用了较短的时间建立了基本完整的工业体系;在改革开放后,我们在全球化背景下、在科教兴国战略的指引下快速地实现了信息化。现阶段我国在信息技术领域的部分细分方向受制于人,部分细分方向进入“无人区”,进一步的长足发展需要我们具有自主创新的勇气和决心,进而需要我们在厘清文化自信的史实的基础上批判继承和整理利用我国古代先进深刻的思想。
2 计算概念谱系化的意义计算概念体系的完备性及准确性,在文化发展和社会交流中具有重要作用。语言是思维的外壳,概念的缺位或粗糙,影响思维的表达。东西方有着不同的历史文化特点,发展进程不完全同步,在计算技术领域也是如此。清末数学家李善兰在翻译西方著作时,首创在汉语中原来并不存在的“微分”“积分”“函数”等名词。物理学家胡刚复教授于1923年将来中国访问的普朗克所说的“ Entropy”翻译为“熵”,这个字在汉语中之前并不存在。计算机科学家夏培肃院士是中文“位”(bit)、“存”(memory)的首次翻译者。诸如此类的概念创新,为汉语世界引入了高频使用的新元素,都具有重要开创意义。如果在汉语中没有这样的概念,或者即使有但不准确,那么很多与这些概念相关的科学研究和文化交流活动将难以像今天这样在中国正常进行。计算概念谱系化,就是建立计算概念的“光谱”,即将原来笼统的计算概念解剖为多个子概念,这些子概念均有客观存在的对应物,而且这些对应物之间的区分与转化十分重要,也正因为这样,谱系化就显得十分必要。
中国古代数学和西方数学代表着计算技术的两个方向、两种风格。中国古代数学达到较高的水平,风格与西方不同。中国古代数学是以问题集的形式出现的,以《九章算术》①为代表;其本质是给出算法,注重实用性、具体性。古希腊数学以第一性原理(First Principles)的形式呈现,以《几何原本》为代表;其本质是证明,注重一般性、抽象性。对比《九章算术》和《几何原本》,可发现前者具体、实用、直白,与实际生活结合紧密;后者抽象、系统、深刻,注重在前件与后件之间建立紧密的逻辑链条。实用通常是优点,因为能立竿见影解决实际问题。但由于过度追求实用而导致放弃研究一般性、抽象性、非功利性问题的时候,实用就演变为实用主义,优点变为缺点。因为这是一种基于趋利的“偷懒”和短视,是一种对自我认知解放机遇的放弃。
① 《九章算术》中包括246个实际问题,分9章论述,故名“九章”。
中国需要自主的计算概念体系。国家主席习近平指出,“文明特别是思想文化是一个国家、一个民族的灵魂。无论哪一个国家、哪一个民族,如果不珍惜自己的思想文化,丢掉了思想文化这个灵魂,这个国家、这个民族是立不起来的”,以及“没有文明的继承和发展,没有文化的弘扬和繁荣,就没有中国梦的实现”。目前,正处于21世纪第3个10年的开端,世界面临百年未有之大变局,我们需要更加坚定不移地坚持文化自信。计算技术是文化的重要组成部分。随着改革进入深水区,与之前长期处于的“跟跑”状态不同,我国在计算领域的更多方向将处于“并跑”或“领跑”状态,有必要将“计算”这样的重要概念中国化,继而将中国的计算概念世界化,培育面向世界的具有中国特色的计算文化,以彰显中国传统文化精华的真理性和卓越性,从而更好地将重要概念沉淀到民族的文化基因中,更好地促进原始创新。
3 计算概念的谱系中国古代数学为算法设计提供了示范。 《九章算术》具有很高的实用性,其中给出了田地面积的计算方法“方田术”、粮食交易或兑换的计算方法“粟米术”、按比例分配的计算方法“衰分术”、由面积或体积求边长的计算方法“少广术”、土石工程中各种立体图形体积的计算方法“商功术”、摊派赋税徭役的计算方法“均输术”、盈亏问题的计算方法“盈不足术”、线性方程组的求解方法“方程术”、直角三角形三边互求的计算方法“勾股术”等实际问题的算法。虽然没有公理化、形式化,但其真理性、原创性毋庸置疑。例如,其第九章提到,“勾股术曰:勾股各自乘,并,而开方除之,即弦。又股自乘,以减弦自乘,其余开方除之,即勾。又勾自乘,以减弦自乘,其余开方除之,即股”。这是勾股定理的完整表述,符号化并翻译成现代汉语即为:设直角三角形三边分别是a、b、c,其中a、b为直角边(勾、股),c为斜边(弦),则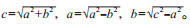
我国古代曾经产生的深刻哲学思想和技术思想,可被用于审视当代的计算技术现状,推动完善计算概念体系。例如,祖冲之在公元5世纪将圆周率估算到小数点后7位,直到16世纪,阿拉伯数学家阿尔· 卡西才打破这一纪录;西周数学家商高在公元前11世纪提出了勾股定理,早于希腊数学家毕达哥拉斯500多年。莱布尼茨创立了二进位制,他于1703年在法国《皇家科学院院刊》发表的《论只使用符号0和1的二进制算术兼论其用途及它赋予伏羲所使用的古老图形的意义》中,确认中国人在3 000年前的《易经》六十四卦里就藏匿了二进位制的奥秘[4]。这些史实说明中国古代曾在数学和自然科学领域有重要发现或创造,也提示中国传统文化中有许多值得挖掘的重要思想或方法,中华文明探源工程具有重要意义。
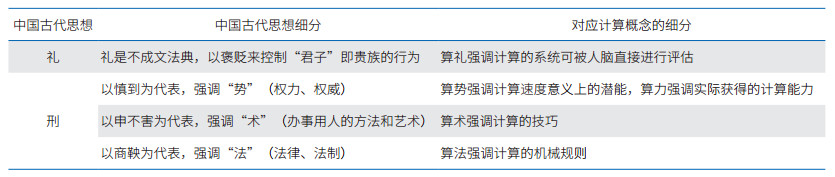
我国古代的哲学思想有助于我们深入理解计算概念的内涵、重新梳理建立计算概念的体系。社会的运行与治理的过程,本身类似于计算的过程,具有并发、秩序等属性,因此古代先贤的社会思想有可能被借鉴于计算技术领域。冯友兰在《中国哲学简史》中对中国古代哲学思想进行了系统的归纳梳理,其中在第14章[5]有这样的总括性表述:“西周封建社会根据两条原则办事,一条是‘礼’,一条是‘刑’。礼是不成文法典,以褒贬来控制‘君子’即贵族的行为。刑则不然,它只适用于‘庶人’,即平民。所以《礼记》中说的:‘礼不下庶人,刑不上大夫。’”这里实现了二分类,其中“刑”是法家的研究对象,又可以一分为三;冯友兰[5]进而指出,“韩非是法家最后的也是最大的理论家,在他之前,法家已经有三派,各有自己的思想路线。一派以慎到为首,慎到与孟子同时,他以‘势’为政治和治术的最重要的因素;一派以申不害为首,强调‘术’是最重要的因素;一派以商鞅为首,最重视‘法’。‘势’指权力、权威,‘法’指法律、法制,‘术’指办事、用人的方法和艺术,也就是政治手腕”。韩非认为,“这三者都是不可缺少的”。
与上述历史思想相对应(表 1),计算概念可以细分为多个组分,分别是算势(computational potential)、算力(computational power)、算术(computational arithmetic)、算法(computational algorithm)、算礼(computational ritual),它们构成了计算概念的谱系。通过这个谱系,能够深刻地、全面地理解和把握计算概念内涵本身所具有的各个方面及其相互关系。这5个组分中,算礼具有鲜明的中国文化特点,算势与算力做了区分,算法与算术做了区分;这些区分能够清晰地反映计算技术领域的痛点,有助于讨论解决这些痛点对应的挑战性问题。
|
算势是某种理想状态或条件下最大的潜在计算能力,不同数量级的算势所能求解的问题复杂度也有数量级的差异。作为法家“势”派的代表,“慎子曰:飞龙乘云,腾蛇游雾,云罢雾霁,而龙蛇与蚓蚁同矣,则失其所乘也”[6]。意思是,法家“势”派的代表人物慎到说:飞龙乘云飞行,腾蛇乘雾游动,然而一旦云开雾散,它们未免就跟蚯蚓、蚂蚁一样了,因为它们失去了腾空飞行的凭借。待求解问题与计算能力之间的关系,就像飞龙与云彩之间的关系一样。
算势是社会生产力的一个重要指标,足够的算势是应用程序或计算任务能够运行的基础。据《2020全球计算力指数评估报告》显示,计算力指数平均每提高1个百分点,数字经济和国内生产总值(GDP)将分别增长0.33% 和0.18%。2016年,谷歌旗下DeepMind公司研发的人工智能机器人阿尔法围棋(AlphaGo)横空出世,击败了世界著名围棋棋手李世石,技惊四座。但不能忽视的是,训练AlphaGo花费了约3 500万美元的计算资源。2018年,谷歌提出3亿参数的双向语言表征模型(BERT),将自然语言处理推向了一个前所未有的新高度,但仍然是以足够的计算能力作为基础。
每一个量级的算势对应一个可求解的问题域(以下简称“可解域”);随着算势增大,可解域也在增大(图 1)。对于算势A和算势B,它们对应的可解域分别是QA和QB,若A<B,则(QB—QA)所包括的是算势B能够求解而算势A不能够求解的问题。(QB—QA)体现了算势增加对求解某些问题所具有的不可替代的使能作用。算势的单位是随应用程序而变化的。例如:对浮点操作密集型应用程序来说,算势的单位是“浮点操作数每秒”(FLOPS);对于事务处理密集型应用程序来说,算势的单位是“事务数每秒”(TPS)。

|
| 图 1 可解域随着算势的增加而不断膨胀 Figure 1 Solvable domain expands as computational potential increases |
算势是因时因地而变的——每个时代有自己的算势,每个国家或地区有自己的算势。 2022年我国提出并开始实施“东数西算”工程,该工程与“西气东输”“西电东送”“南水北调”等一样都是资源跨域调配战略工程。针对我国东、西部算势分布总体呈现出“东部不足、西部过剩”的不平衡局面,引导中西部利用能源优势建设计算基础设施——“数据向西,算力向东”,服务东部沿海等算力紧缺区域,以解决我国东西部算势分布不均衡、供需不平衡的问题。
算势的概念可以促进我们理解经典串行计算、经典并行计算、量子计算之间的联系和区别:经典并行计算(或超级计算)相对于串行计算,是为了增加算势;量子计算相对于经典计算,也是为了增加算势。夏培肃院士毕生后投身于研制高性能经典计算机的实践,她的丈夫杨立铭院士毕生从事理论物理的研究,先后培养了曾瑾言、钱伯初等量子力学教育家。他们无论是做工程实践,还是做理论研究,无论是做经典计算机,还是做量子计算机,从根本上说都是为了增加算势。需要指出,一方面,经典并行计算、量子计算能极大地提高算势;另一方面,1936年图灵研究判定性问题时所提出的图灵机模型是串行的[7]。但经典并行计算、量子计算不会改变问题的不可求解性;也就是说,如果一个问题在串行图灵机上是不可求解的,那么通过经典并行计算、量子计算仍然不可解(图 1)。
3.2 算力算力是应用程序所能实际获得的计算能力,其上界是算势,来源于算势,受限于算势,但不等同于算势;如何弥合两者之间的鸿沟,实现从算势到算力的高效转化,是包括计算机系统结构和系统软件在内的整个计算机学科需要研究解决的核心问题。算势转化为算力的过程依赖很多条件或因素,如应用程序的特征、运行环境的特征、多处理器之间负载是否均衡等。一方面,要注意算势的基本限制作用,尽量提高算势;另一方面,要注意算势向算力的充分转化,尽量充分利用算势。这2个方面目标一致,不可偏废。
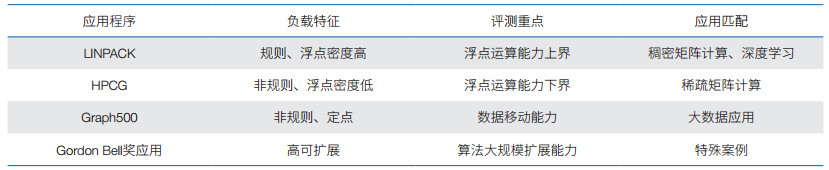
各种类型的计算机都存在算势向算力转化不充分的问题(表 2)。例如,在超级计算机上,普通用户的很多程序往往效率较低。2022年图灵奖得主杰克·唐加拉参与编制的线性系统软件包(LINPACK)成为评测超级计算机的工具,但该工具只代表较为理想的情况,因为其中包含良好的局部性、易开发的并行性特点的大量稠密矩阵计算。基准测试程序(HPCG)则代表了大量实际应用中常出现的不易扩展和开发局部性的稀疏计算和访存模式。测试基准Graph500代表了数据密集型应用的情况。戈登· 贝尔(Gordon Bell)奖应用则代表了算法优化所能带来的效率提升。
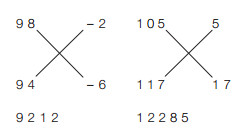
算术是关于数值的算法,是狭义的算法,也是最基本、最顾名思义的算法。算术强调四则运算、开方、乘方等计算的技巧。例如,冯· 诺伊曼在1945年的EDVAC研制报告中就用了多个章节分别讨论了这些方面[9],以及中国乘法和印度乘法就使用了不同的技巧。以2位数和3位数乘法为例,中国乘法建立在逐位相乘的基础上(图 2);印度乘法建立在求差值的基础上,将对角线上的数字之和作为结果的高位,将差值的乘积作为结果的低位(图 3)。从中可以直观地感受到中国乘法和印度乘法使用了不同的技巧。

|
| 图 2 中国乘法算术 Figure 2 Chinese multiplication arithmetic |
|
| 图 3 印度乘法算术 Figure 3 Indian multiplication arithmetic |
算法是广义的计算方法,包括数值算法、非数值算法,强调计算的机械的规则。吴文俊等创立和发展了数学机械化[3]。只有机械化,才能由计算机自动去执行。几何定理的证明分为2个步骤:①几何的代数化与坐标化。从几何的公理系统出发,引进数系统与坐标系统,使得任意几何定理的证明问题成为代数问题。②几何的机械化。将几何定理假设部分的代数关系式进行整理,然后按照确定步骤(编写为程序)验证定理终结部分的代数关系式是否可以从假设部分已整理成序的代数关系式推出。
尽管算法是由人脑设计,但人脑本身不善于执行机械的规则;同时,大量的问题往往通过机械的规则(即通过算法而不是巧思)更容易解决。人脑善于巧思,但不善于反复枯燥的操作,这可能与人脑本身所具有的多巴胺等物质比较稀缺,以及独特的奖励惩罚机制有关。以几何为例来说明,几何分为综合几何和解析几何。综合几何就是我国初中所教授的几何,其解题往往需要观察、“巧妙”地添加辅助线,也就是需要人脑的巧思。借助图形的直观形象,以一些基本名词(如点、直线、平面等)和关系(如衔接、顺序、相似等),满足一套公理或公设,经过一定的逻辑推理,导出一系列的定理的研究方法,被称为古典公理法或综合法,而用这种方法所研究的几何被称为综合几何。综合几何与17世纪笛卡尔创立的解析几何相对。吴文俊指出,综合几何尽管直观生动,但使用范围“颇为有限”,相反解析几何应用范围很广。
算法强调2个方面,且需要具备5个特征。 2个方面为:①功能——能否计算;②性能——能以多快的速度计算。5个特征为:①有穷性(finiteness)——必须在有限的步骤内终止;②确定性(definiteness)——每一步骤必须被精确地、严格地定义,不能有歧义性;③输入(input)——有0个或多个输入;④输出(output)——至少有1个输出;⑤能行性(effectiveness)——所涉及的操作必须足够基本,以致操作在原理上能被人用铅笔和纸在有限的时间内完成。
以上5个特征之中的能行性涉及一个内容深刻的重要学科方向——可计算性理论[4]。可计算性理论是很多计算机从业者较为欠缺的。可计算性理论有很多结论是与没有经过这方面训练的人的直觉相反的,这样的结论实例有:①可计算的本质是递归;②算法的数量是可数的(而实数的数量是不可数的);③不存在一般过程能够在有限步内判定一个计算过程是否是算法。一个给定的问题是否存在对应的算法,是一个关于“是否可解”的问题。如果存在对应的算法,怎样找出或构造出这个算法,是一个关于“如何求解”的问题;这往往涉及人类对于问题所处领域的理解,也就是通常所说的“ know-how”,即技术诀窍、专业知识、私家配方(“秘方”)。
计算机、算法都是人脑设计的,人工智能归根结底是人类智能的外化(externalization)和自动化(automation)。钱学森在1957年发表的《论技术科学》[3]中阐述,“......技术科学工作中最主要的一点是对所研究问题的认识。只有对一个问题认识以后才能开始分析,才能开始计算。但是什么是对问题的认识呢?这里包含确定问题的要点在哪里,什么是问题中现象的主要因素,什么是次要因素;哪些因素虽然也存在,可是它们对问题本身不起多大作用,因而这些因素就可以略而不计。要能做到这一步,我们必须首先做一些准备工作,收集有关研究题目的资料,特别是实验数据和现场观察的数据,把这些资料印入脑中,记住它,为做下一阶段工作的准备,下一个阶段就是真正创造性的工作了。创造的过程是:运用自然科学的规律为摸索道路的指南针,在资料的森林里,找出一个道路来。这条道路代表我们对所研究的问题的认识,对现象机理的了解。也正如在密林中找道路一样,道路决难顺利地一找就找到,中间很可能要被不对头的踪迹所误,引入迷途,常常要走回头路......把问题认识清楚以后,下一步就是建立模型......有了模型了,再下一步就是分析和计算了……”。
上面描述的就是人脑构思或构造算法的过程。算法的构思或构造处于人类认识客观世界的最前沿,算法离不开人脑所进行的“创造性的工作”,实际上“希尔伯特计划”失败的原因就在于此,即判定性问题的答案是否定的[7];也就是说,不存在一般过程能够在有限步内判定一个计算过程是否是算法。
3.5 算礼人脑与计算机之间存在着紧密联系,又存在着内在机制和语义沟通上的鸿沟。人脑具有与计算机不同的特点。相对计算机,人脑有直觉、大局观,但不善于快速精确计算和记忆。计算机又称电脑,是实现或执行人工智能算法的载体;同时,人工智能算法又可以用来设计计算机,于是就出现了用电脑设计电脑的现象。但就根源来说,计算机、人工智能算法都是人脑的设计结果,而设计过程本质上是计算。但是,对大多数研究和设计人员来说,计算机系统长期以来是一个“黑箱”,缺乏可分析的抽象,人脑很难精确、全面地分析。以深度学习为代表的很多人工智能算法存在一个长期以来为人诟病的弊端:人工智能算法是一个“黑箱”,可解释性、透明性、可分析性不强。人脑设计的产物反而不能被人脑理解,这成为一个亟待破解的悖论。
算礼是关于计算如何在计算机系统上进行的制度规范;其比算法更接近人脑这一端,更关注计算机系统的整体,强调计算的系统可被人脑直接进行评估[8]。算法是关于单一应用内部计算方法的说明,聚焦于应用个体;算礼除了考虑每个算法之外,还考虑运行在同一系统之上的多个算法之间的协调有序,聚焦于系统整体。高通量计算、低熵数据中心都体现了这一点。高通量计算并不关注单个应用或单个请求的性能,而是关注大批量高并发的应用或请求的整体吞吐量;对个体应用而言,其性能相比于理想时(即单独运行时)一般变差了,但相对低通量时的排队延迟导致的不可服务性来说,性能有了很大的提升。
算礼是不成文的,相对算法而言是软性的,但其褒贬意义上的影响力不可替代。褒贬就是评估(evaluation),通过褒贬,社会系统之中多个主体之间的关系得到调节和规范,社会系统在很多发展可能之中筛选出符合礼的那一种。在西周时期,周王室与诸侯国之间“保持着社会的、外交的接触,如果有什么事情要处理,也都遵循他们不成文的‘君子协定’。这就是说,他们是尊礼而行”[5]。法的执行往往需要较大的时间成本和资源成本,原型系统实现和基准程序测试也往往需要较大的时间成本和资源成本。一方面,设计空间和应用空间都极其庞大,进而设计空间与应用空间的笛卡尔积更加庞大;另一方面,原型系统实现和基准程序测试的缓慢。两者造成尖锐的矛盾,增大了实现应用程序与系统结构之间良好匹配的难度。因此,需要通过算礼,在原型系统实现和基准程序测试之前,就能够分析出该系统的主要性质,进而筛掉不合适的候选系统,大幅度提高设计敏捷度,加速人类智能向人工智能的转化、外化、物化的过程。
算礼的必要性毋庸置疑,算礼的可行性需要加强研究。算礼要解决的是:不依赖机器条件下,如何开展计算机这样的复杂系统的顶层设计。需要解决人脑思维所需要的元素的命名与抽象问题,要能反映计算机系统的实际状况,又要便于人脑记忆与推理。诸如模型、分治、分层、模块化、经验法则等思想或技术可以被运用此过程,以使能或加速人脑进行系统顶层设计和敏捷开发。
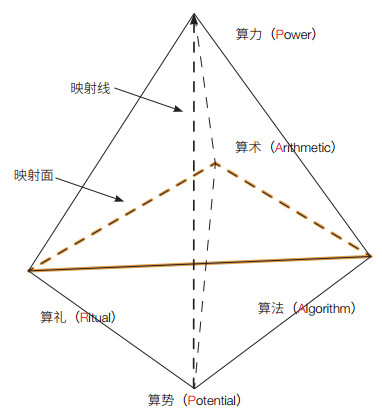
4 计算概念谱系组分的相互关系计算概念谱系将计算概念的内涵细分,形成一个立体的相互联系的有机整体(图 4)。算势、算力、算术、算法、算礼是同一事物(计算)的不同方面,它们有着不同的侧重点,又有着相同的目的或价值取向,即为了计算系统更快、更好地完成待求解的应用问题。图 4是一个三角双锥,算术、算法、算礼3个因素构成一个三角形,本质上是计算的映射面,其上部和下部各有一个顶点,下部顶点是算势,上部顶点是算力,算势向算力的转化是计算的主线(映射线),计算的映射面的状况决定了算势向算力的转化率。
|
| 图 4 计算概念谱系 Figure 4 Computation concept genealogy |
算礼是算法的前序,算法是算术的推广,算势是算力的基本限制。我们需要攻克高端光刻机技术,不断地改进工艺,扩大算势;同时,我们要通过跨层垂直优化[10]等技术提高算势向算力的转化率,在算势不变或增加缓慢时,仍可获得较高的算力。
算势与算术、算法之间有着微妙的互补或替代关系。例如,当算势足够大的时候,算势的强大可以弥补算术的笨拙,所以此时算术或算法技巧的巧妙高明未必很重要,只起到锦上添花的作用;当算势不充分的时候,如由于芯片制造工艺被“卡脖子”或者由于东西部算势不均衡,算术或算法性能优越就非常必要,应起到雪中送炭的作用。
人工智能来源于人,又最终服务于人,因此计算的内涵在各个方面、环节之间的转化率问题至关重要。算礼关注人类智能向人工智能的转化、建立人脑与电脑之间的桥梁,算法关注输入与输出之间的转化过程、建立已知与未知之间的桥梁,算礼与算法均提供转化可能、提高转化效率。算势与算力之间有着不同程度的鸿沟,存在着转化的问题。算力与满足人类日益增长的美好生活需要之间也存在着鸿沟,也存在着转化的问题。
5 结束语计算概念具有重要作用,需要我们建立清晰的谱系以彰显其丰富的内涵。计算概念的中国化是增强文化自信的重要步骤。坚定的自信需要建立在,也只能建立在对客观史实、客观真理的理性认知基础上。真理是无国界的,西方计算概念的中国化与中国计算概念的世界化同时发生、相向而行、相互补充。将中国传统思想文化的优秀部分与现代科技的重要概念无缝衔接起来,有助于发扬和彰显传统文化的真理性,同时也有助于使用传统文化词汇来思考现代科技问题。中国古代基于时间长度、人口数量、文明高度,积累了巨大的历史遗产;中国历史上存在的数以亿万计的人脑(即祖先的大脑)计算或思索的成果形成了一个宝库,在核心技术“卡脖子”、人口老龄化等国内外危机叠加频发的背景下,尤其值得并需要当代人挖掘、整理和提高。
| [1] |
吉尔多维克. 计算进化史. 劳佳, 译. 北京: 人民邮电出版社, 2017. Gildovik. Evolutionary History of Computation. Translated by Lao J. Beijing: Posts and Telecommunications Press, 2017. (in Chinese) |
| [2] |
钱学森. 论技术科学. 科学通报, 1957, 2(3): 97-104. Qian X S. Science of technology. Chinese Science Bulletin, 1957, 2(3): 97-104. (in Chinese) |
| [3] |
吴文俊. 几何定理机器证明的基本原理: 初等几何部分. 北京: 科学出版社, 1984. Wu W J. Basic Principles of Machine Proof of Geometric Theorems: Elementary Geometry. Beijing: Science Press, 1984. (in Chinese) |
| [4] |
蔡天新. 数学传奇: 那些难以企及的人物. 北京: 商务印书馆, 2016. Cai T X. Legends of Mathematics: Those Hard to Reach Figures. Beijing: The Commercial Press, 2016. (in Chinese) |
| [5] |
冯友兰. 中国哲学简史. 涂又光, 译. 北京: 北京大学出版社, 2013: 150-153. Feng Y L. A Short History of Chinese Philosophy. Translated by Tu Y G. Beijing: Peking University Press, 2013: 150-153. (in Chinese) |
| [6] |
韩非. 韩非子·难势. 北京: 中华书局, 2015. Han F. Han Feizi·Heckling Potential. Beijing: ZHONGHUA BOOK COMPANY, 2015. (in Chinese) |
| [7] |
Turing A M. On computable numbers, with an application to the entscheidungsproblem. Proceedings of the London Mathematical Society, 1936, 42: 230. |
| [8] |
徐志伟, 王一帆, 赵永威, 等. 算礼: 探索计算系统的可分析抽象. 计算机研究与发展, 2020, 57(5): 897-905. Xu Z W, Wang Y F, Zhao Y W, et al. Computation protocols: Analyzable abstractions for computing systems. Journal of Computer Research and Development, 2020, 57(5): 897-905. (in Chinese) |
| [9] |
John V N. First Draft of a Report on the EDVAC. University of Pennsylvania. (1945-06-30)[2022-05-13]. https://page-one.springer.com/pdf/preview/10.1007/978-3-642-61812-3_30.
|
| [10] |
孙凝晖. 对信息技术新体系的思考. 中国科学院院刊, 2022, 37(1): 8-14. Sun N H. Thoughts on new IT technique system. Bulletin of Chinese Academy of Sciences, 2022, 37(1): 8-14. (in Chinese) |